ヘイブリッジ

ヘイブリッジとは、4つの抵抗器と1つのキャパシタと1つのインダクタをブリッジ型に配置する回路のことである。 ブリッジ回路の1種である。

概要

既知の抵抗器の抵抗値やキャパシタのキャパシタンスで、未知のものの抵抗値やインダクタンスあるいは周波数を測定するための回路である。

平衡条件

平衡条件というのは、下記回路図で言うと、電位差$V$を$V=0$にするということである。

回路図

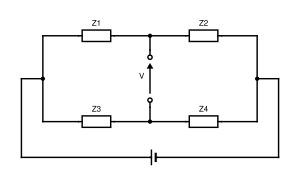
一般にブリッジ回路では

$Z_{1}Z_{4}=Z_{2}Z_{3}$

と対角線同士をかけたものが同じになる関係が成り立つ。 これは、$V=0$より、電圧が分圧される比が等しいということ($Z_{1}:Z_{2}=Z_{3}:Z_{4}$)から導かれる。

以下角周波数を$\omega$として表す。
ヘイブリッジでは

• $Z_{1}$が抵抗$R_{1}$とインダクタ$L_{1}$の直列接続で$Z_{1}=R_{1}+j\omega L_{1}$
• $Z_{2}$が抵抗$R_{2}$のみで$Z_{2}=R_{2}$
• $Z_{3}$が抵抗$R_{3}$のみで$Z_{3}=R_{3}$
• $Z_{4}$が抵抗$R_{4}$とキャパシタ$C_{4}$ので直列接続$Z_{4}=R_{4}+{\frac {1}{j\omega C_{4}}}$

であるので

$\left(R_{1}+j\omega L_{1}\right)\left(R_{4}+{\frac {1}{j\omega C_{4}}}\right)=R_{2}R_{3}$

となる。これを整理して

$\left(R_{1}+j\omega L_{1}\right){\frac {1+j\omega C_{4}R_{4}}{j\omega C_{4}}}=R_{2}R_{3}$

分母をはらって

$\left(R_{1}+j\omega L_{1}\right)\left(1+j\omega C_{4}R_{4}\right)=j\omega C_{4}R_{2}R_{3}$

これを実部と虚部をそれぞれ比較しやすいようににすると

$(R_{1}-\omega ^{2}L_{1}C_{4}R_{4})+j\omega (L_{1}+C_{4}R_{1}R_{4}-C_{4}R_{2}R_{3})=0$

これの実部より

$R_{1}=\omega ^{2}L_{1}C_{4}R_{4}$

また、虚部より

$L_{1}+C_{4}R_{1}R_{4}=C_{4}R_{2}R_{3}$

よって、平衡条件は

${\begin{cases}R_{1}=\omega ^{2}L_{1}C_{4}R_{4}\\L_{1}+C_{4}R_{1}R_{4}=C_{4}R_{2}R_{3}\end{cases}}$

となる。これより(角)周波数と$R_{2},R_{3},R_{4},C_{4}$が既知であれば$R_{1},L_{1}$を求めらる。 具体的には、第一式を第二式に代入して$L_{1}$を得て、それを$R_{1}$に代入して

${\begin{cases}L_{1}={\frac {C_{4}R_{2}R_{3}}{1+\omega ^{2}C_{4}^{2}R_{4}^{2}}}\\R_{1}=\omega ^{2}L_{1}C_{4}R_{4}={\frac {\omega ^{2}C_{4}^{2}R_{2}R_{3}R_{4}}{1+\omega ^{2}C_{4}^{2}R_{4}^{2}}}\end{cases}}$

逆に$R_{1},R_{4},C_{4},L_{1}$が既知であれば(角)周波数を求められることが分かる。

$\omega ={\sqrt {\frac {R_{1}}{L_{1}C_{4}R_{4}}}}$

関連項目

• ホイートストンブリッジ
• キャパシタンスブリッジ
• 直列キャパシタンスブリッジ
• シェーリングブリッジ
• ウィーンブリッジ
• マクスウェルブリッジ
• オーウェンブリッジ
• ヘビサイドブリッジ
• コールラウシュブリッジ
• アンダーソンブリッジ