単振動

物理学のニュートン力学に於ける単振動とは壁に固定したばねに物体を繋いで引っ張った時に生じる左右の振動及びそれに類似した振動である。

概要

上述のよーな運動を行ったとき横方向の距離を$x$、横方向の外力を$F_x$とおくと以下のフックの法則が成り立つ(比例定数のkは「ばね定数」と呼ばれている)。；

$F_x=-kx$

この法則にニュートンの運動方程式を代入すると

$m\ddot{x}=-kx$

となる。ここで${\omega }^2=k/m$とおけば上記2階線形微分方程式は

$\ddot{x}+{\omega }^{2}x=0$

と書ける。この微分方程式の特性方程式は

${\alpha }^2+{\omega }^2=0$

であり、解くと$\alpha =\pm i\omega$が得られる。従って上記微分方程式の一般解は次式で与えられる。；

$x=c_1\cos \omega t+c_2\sin \omega t$

更に$c_1=A\sin {\theta }_0,c_2=A\cos {\theta }_0$とおけば上記の一般解は

• $x(t)=A\sin (\omega t+{\theta }_0)$

と表わせる。

上述の解の係数Aを振幅といい正弦の中身を位相と呼ぶ。特に${\theta }_0$は時刻tが零のときの位相なので初期位相と呼ばれる。

上記の解の独立変数tをt+Tに置き換えたら

$\begin{array}{rl}x(t+T)& =A\sin (\omega (t+T)+{\theta }_0)\\ & =A\sin (\omega t+{\theta }_0+\omega T)\end{array}$

となるが正弦関数は周期2πの周期関数であるから 上述の単振動の公式に対して

$x(t)=x(t+T)$

とゆー周期関数の性質が成り立つためには上式の$\omega T$に関して以下の如き関係式

$\omega T=2\pi$

が成り立たねばならない。ここで現れた物理量Tを(時間的な)周期という。従って

• $\omega =\frac{2\pi }{T}$

とゆー等式が成立する。

ところで単位時間当たりの振動の回数を振動数(または周波数)といいνで表わすんだが1回振動するのにかかる時間が周期Tなんだから振動数と周期には以下の関係が成り立つ事になる。；

• $\nu =\frac{1}{T}$

これより以下の如き公式が導かれた事になる。；

• $\omega =2\pi \nu$

上述のωは角振動数と呼ばれている物理量である(※これは円運動に於ける角速度と同様の概念だったりする)。

※ちなみに振動数の単位は「Hz(ヘルツ)」、角振動数の単位は「rad/s(ラジアン毎秒)」と呼ぶ。

単振動のエネルギー

上記一般解の角度をφとおいて微分したら

$\dot{x}=-A\omega \cos \varphi$

となるが、これを運動エネルギーの公式に代入したら

$K=\frac{1}{2}m{\dot{x}}^2=\frac{1}{2}m{\omega }^2{A}^2{\cos }^2\varphi$

となる。また$F_x=-m{\omega }^{2}x$と位置エネルギーの公式より

$\begin{array}{rl}U& =-\int F_{x}dx=\int m{\omega }^{2}xdx=\frac{1}{2}m{\omega }^2{x}^2\\ & =\frac{1}{2}m{\omega }^2{A}^2{\sin }^2\varphi \end{array}$

が得られる。これらを力学的エネルギー保存則

$K+U=E$

に代入したら以下の如く単振動のエネルギーが導かれる。；

• $E=\frac{1}{2}m{\omega }^2{A}^2$

従って単振動のエネルギーは角振動数の2乗と振幅の2乗に比例する。

単振り子

振り子の微小に振動させると、その運動は単振動で近似できる。 このとき、振り子の等時性が成立し、振動が微小であれば振り子の周期は一定となる。 $T=2\pi \sqrt{\frac{l}{g}}$(単振り子の周期$T$は、振り子の長さ$l$と重力加速度$g$にのみ依存する) 1mの振り子では約1秒で半周期分の運動をする。そのため、 $1[s]=\pi \sqrt{\frac{1[m]}{g}}$ となって、これから重力加速度を計算すると、 $g={\pi }^2[m/s^2]$ のように、円周率の2乗になる。 これは偶然ではない。 地球の周長の四千万分の1(=地球の北極点から赤道までの子午線距離の一千万分の1)を1mと定める以前の、mの定義はこの振り子の等時性を利用した定義であった。振り子の半周期が1秒になるような長さを1メートルと定めていた。 その後幾度かの改訂によって1mの定義は変化したが、大きくずれないようにして改訂された。 そのため、重力加速度≒円周率の2乗となっている。(ただし、重力加速度も地球のどこにいるかで少し変わるし、円周率は3を主張する者もいる。) なお現在のSIでは、mを光速を使って定義している。

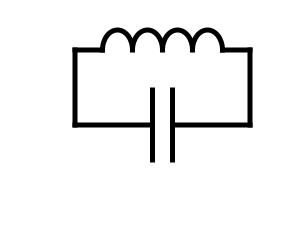
LC共振回路

インダクタとキャパシタを接続した回路に、初期値として非零の電圧や電流を与えると、単振動を起こす。 このLC共振は、バネと質点の運動と同じ形をもつ微分方程式で記述される物理現象である。

LC共振回路

バネや質点に空気抵抗などダンパー(減衰成分)がつくことは、電気抵抗がつくことに対応し、どちらの現象も実際にはこれらの成分があるので、徐々にエネルギーを失って減衰する。 両者の対応関係を以下に示す。

バネマス(ダンパ)系	(R)LC共振回路	役割など
変位$x$(位置エネルギーをためる)	電荷$Q$(静電エネルギーをためる)	振動するもの(これをXとする)
速度$v=\frac{d}{dt}x$(運動エネルギーをためる)	電流$I_C=\frac{d}{dt}Q$(磁気エネルギーをためる)	Xの微分
力$F=m\frac{d}{dt}v=-kx-\beta v$	電圧$V_L=-L\frac{d}{dt}{I}_C=Q/C+R{I}_C$	Xの2回微分
質量$m$	インダクタンス$L$	Xの微分を一定にしようとする(動きにくさ)
減衰係数$\beta$	電気抵抗$R$	エネルギーを消費して減衰させる(損失)
ばね定数$k$	キャパシタンスの逆数$1/C$	Xを逆方向に動かす
$m\frac{d^{2}x}{d{t}^2}+\beta \frac{dx}{dt}+kx=0$	$L\frac{d^{2}Q}{d{t}^2}+R\frac{dQ}{dt}+\frac{1}{C}Q=0$	微分方程式
$\omega =\sqrt{k/m}$	$\omega =\sqrt{1/LC}$	損失ゼロでの角振動数(角周波数)$\omega$
$T=2\pi \sqrt{m/k}$	$T=2\pi \sqrt{1/LC}$	損失ゼロでの周期$T=2\pi /\omega$
$x=C_1\sin (\omega t)+C_2\cos (\omega t)$	$Q=C_1\sin (\omega t)+C_2\cos (\omega t)$	損失ゼロでの微分方程式の解

このように、バネマス(ダンパ)系、(R)LC共振回路ともに、全エネルギーが2種類の形態を行ったり来たりする振動である。 言うならばmとk,Lと1/Cのせめぎ合いであり、損失ゼロのときの角振動数や周期に表れている。 質量が重い質点では速度が変化しづらく、バネが強いと速度が変化しやすい。 同じように、大きなインダクタでは電流が変化しづらく、小さなキャパシタでは電流が変化しやすい。

関連項目

• 自由振動
• 強制振動
• 減衰振動
• 固有振動
• 共振
• 非線形振動
• 電気機械音響類似