電気抵抗

	意見募集
	このページの内容について意見を募集しています。議論は「トークページ」で行われています。

電気抵抗 (でんきていこう)は、電流の流れにくさのこと。レジスタンスや抵抗ともいう。

概要[編集]

オームの法則(E=IR。覚え方、伊勢鉄道(IRはいい)或いはV=RI)によると、電気抵抗は電圧と電流の比例係数になっている。数式中で抵抗を表すときはRとr(内部抵抗)で表記する。

電池の内部抵抗[編集]

電流を流していない電池の両極間の電位差を電池の起電力という。この電池に抵抗を接続すると電池の内部で抵抗を生ずる。これを内部抵抗ｒという。電流Iが流れると電池内部で電圧降下rI[V]が起き、電池の両極間の電位差は起電力よりも低くなる。この低くなった電圧V[V]を端子電圧という。EとVの関係は次の式で表される。

V=E-rI　または　E=V+rI　

これをオームの法則、V=IRに代入すると

E=(R+r)I

となり、Rとrは抵抗の直列接続として働く。

微分抵抗と負性抵抗[編集]

電流と電圧の関係が線形でない場合は、電圧の電流微分を取った値を微分抵抗と呼び、これを取り扱うこともある。例えば、半導体素子では微分抵抗を利用する。微分抵抗が負になるときは、負性抵抗(負性微分抵抗)と呼ばれる。

直流抵抗と交流抵抗[編集]

(1) 直流抵抗は抵抗率と長さ(電流を流す向き)に比例し、断面積に反比例する。

抵抗率について。
- 抵抗は、導線の長さｌに比例し、断面積Sに反比例する。ここに比例定数をρとし、R(Ω)、ρ(m･Ω)、l(m)、S(m²)とすると

R=\rho {\frac {l}{S}}

が成り立つ。

比例定数ρはその導線の材質の抵抗率という。ρは導線の長さが1m、その断面積が1m²あたりの電気抵抗である。

(2) 交流抵抗(インピーダンス)は一般に複素数を取る。インピーダンスが複素数を取ることや半導体素子とエネルギー源を利用して、外部から見て負性抵抗をもつように見える回路も作成できる。

交流回路[編集]

直列回路[編集]

抵抗値R[Ω]の抵抗、自己インダクタンスL[H]のコイル、電気容量C[F]のコンデンサーの直列回路に、周波数f[Hz]の交流電源を入れると、回路を流れる電流の最大値I_o[A]はオームの法則より

$I_{o}={\frac {V_{o}}{Z}}$

ただし、

$Z={\sqrt {R^{2}+({\omega }L-{{\frac {1}{{\omega }{C}}})^{2}}}}$

上の式で、抵抗Ｒ、コイルＣ、コンデンサＣの中でないものがあれば、インピーダンスＺの式の中から不要なものを除去すればいい。すなわち

①抵抗ＲとコンデンサーＣのみの回路の場合

$Z={\sqrt {R^{2}+{\frac {1}{({\omega }{C})^{2}}}}}$

②抵抗ＲとコイルＬのみの回路の場合

$Z={\sqrt {R^{2}+({\omega }{L})^{2}}}$

となる。ｚ[Ω]は交流回路で全体の抵抗の働きをする量として複素数で表せる。これを複素インピーダンス、もしくは単にインピーダンスといい、この逆数をアドミタンスという。このアドミタンスはＹで表される。また、

$({\omega }L-{\frac {1}{{\omega }{C}}})$ 　　[Ω]

はインピーダンスの虚数部であり、回路全体の(抵抗に対して)リアクタンスと呼ばれ、一般にＸで表される。

名称	意味	記号
インピーダンス	交流回路の抵抗を複素数で表した	Ｚ
アドミタンス	インピーダンスの逆数	Ｙ
リアクタンス	インピーダンスの虚数部	Ｘ

詳細は「交流#抵抗・インダクタンス・キャパシタンス」を参照

影響[編集]

電荷が電気抵抗を流れると、電位が下がり、電気エネルギーが失われる。失われたエネルギーは、通常熱エネルギーに変化し、抵抗が発熱する。電化製品を使うと発熱するのは、電気抵抗が原因である。

スマートフォンなど、モーターを使わない電化製品の消費電力は、ほぼ電気抵抗によるものである。なおドライヤーなど、熱を発生させることが目的の電化製品の場合、積極的に電気抵抗にかける電圧を高くしている。

抵抗を含む機器を商用電源につないだ場合、失われた電気エネルギーがメーターに記録され、電力会社から電気代を請求される。また、発電機のタービンにブレーキがかかるので、発電所では回転速度を落とさないためにタービンを回す蒸気圧を上げようとして、燃料をより多く燃やすことになる。

電線も含め、あらゆる物質が電気抵抗を含んでいる。電気抵抗が小さいほど省エネになる。近年は、極低温にすることにより電気抵抗ゼロを目指す動きもあり、電気抵抗ゼロのことを超伝導と呼ぶ。

単位[編集]

国際単位系 (SI) において、抵抗の大きさを表す単位はオームであり、単位記号はΩである。また、抵抗の逆数をコンダクタンスと言い、電流の流れやすさを表す。コンダクタンスのSIにおける単位はジーメンスであり、単位記号はSである。

電気回路における抵抗値の計算[編集]

直列接続[編集]

直列接続された抵抗全体の抵抗値は、各抵抗値の総和になる。

R=\sum _{i}r_{i}

これは、抵抗が長さに比例することと本質的に同じである。
2つの抵抗 $r_{1},r_{2}$ を並列接続したものの抵抗値は $r_{1}+r_{2}$ である。

例えば2Ωと3Ωの抵抗を直列接続したら5Ωとなる。

並列接続[編集]

並列接続された抵抗全体の抵抗値は、各抵抗値の{(逆数の総和)の逆数}になる。

{\frac {1}{R}}=\sum _{i}{\frac {1}{r_{i}}}

これは、抵抗が断面積に反比例することと本質的に同じである。
逆数の計算を簡略化した表記で、 $a//b={\frac {1}{{\frac {1}{a}}+{\frac {1}{b}}}}={\frac {ab}{a+b}}$ を利用すれば、 2つの抵抗 $r_{1},r_{2}$ を並列接続したものの抵抗値は $r_{1}//r_{2}$ である。(//はパラレル(平行)と呼ぶ。)
例えば2Ωと3Ωの抵抗を並列接続したら1.2Ωとなる。

抵抗で計算すると逆数が入ってしまうため、コンダクタンスを使用することも多く、並列接続された抵抗全体のコンダクタンスは、各コンダクタンスのの総和になる。

G=\sum _{i}g_{i}

対称性の高い場合[編集]

直並列(直列接続と並列接続の組み合わせ)の回路であれば以上の方法で計算できるが、複雑な回路では計算が困難・煩雑になる。
ただし、回路の対称性を利用すれば計算量を減らす工夫ができることもある。しかし、実際の回路では、抵抗値のズレ(公差など)があるので厳密に対称性が高い場面は少ない。

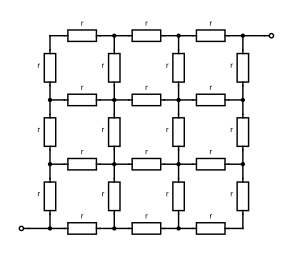
例えば、 $(n+1)\times (n+1)$ の正方形状の格子点について、隣り合う格子点同士をつなぐ各導線上に同一の抵抗が1つずつ配置された回路のある端とその対角にある端の間の抵抗値 $R_{n}$ を考える^[1]。ここで、各抵抗の抵抗値は $r$ とし、抵抗は全部で $2n(n-1)$ 個ある。結論から述べると、全体の抵抗値は漸化式

R_{n+1}=r+(R_{n}//nr),R_{1}=r

に従う。
これを導出するには、対称性から回路を2つ対角線で切り分けた4つの部分(以下1/4の回路と呼ぶ)が直並列(この回路は直列接続が並列接続しているとも言えるし、並列接続が直列接続しているとも言える)しているような回路と等価であることを利用する。すると、この1/4の回路の抵抗値を $R_{n}^{'}$ と置くと、 $R_{n}$ は直列で2倍されて並列で1/2倍されるので、全体の抵抗値は $R_{n}=R_{n}^{'}$ と1/4の回路の抵抗値と同じであることがわかる。
この1/4の回路は $n$ について再帰的に構築されていくので、漸化式で表せる。具体的には、 $R_{n+1}^{'}$ の回路は、[ $r$ と{ $R_{n}^{'}$ の回路と( $n$ 個の $r$ の直列接続)の並列接続}の直列接続]である。(ただ日本語で書いてもわかりにくいのでカッコをつけたが、数式を見た方がわかりやすいだろう。)

R_{n+1}=r+(R_{n}//nr)

また、 $R_{1}^{'}$ の回路は $r$ そのものなので初期条件

R_{1}=r

を満たす。

Y-Δ変換・Δ-Y変換[編集]

三相交流などで使用される、Δ形回路とY形回路は相互に変換可能であり、抵抗値の変換についても良く知られている。詳しくは、Y-Δ変換・Δ-Y変換を参照されたい。

詳細は「交流#三相交流」を参照

出典[編集]

↑ すぶた∫ @情報カンファ代表氏の投稿(ここでは $n=3$ の回路を扱っている)

参考文献[編集]

力武常次、都築嘉弘『チャート式シリーズ新物理ⅠB・Ⅱ』数研出版株式会社新制第11刷1998年4月1日発行
西巻正郎・森武昭・荒井俊彦『電気回路の基礎』森北出版株式会社1998年 3月18日第1版第12刷発行

[1] すぶた∫ @情報カンファ代表氏の投稿(ここでは $n=3$ の回路を扱っている)

[1]

電気抵抗

目次

概要[編集]

電池の内部抵抗[編集]

微分抵抗と負性抵抗[編集]

直流抵抗と交流抵抗[編集]

交流回路[編集]

直列回路[編集]

影響[編集]

単位[編集]

電気回路における抵抗値の計算[編集]

直列接続[編集]

並列接続[編集]

対称性の高い場合[編集]

Y-Δ変換・Δ-Y変換[編集]

関連項目[編集]

出典[編集]

参考文献[編集]

ナビゲーションメニュー

電気抵抗

概要[編集]

電池の内部抵抗[編集]

微分抵抗と負性抵抗[編集]

直流抵抗と交流抵抗[編集]

交流回路[編集]

直列回路[編集]

影響[編集]

単位[編集]

電気回路における抵抗値の計算[編集]

直列接続[編集]

並列接続[編集]

対称性の高い場合[編集]

Y-Δ変換・Δ-Y変換[編集]

関連項目[編集]

出典[編集]

参考文献[編集]

ナビゲーション メニュー

検索

ナビゲーションメニュー