Y-Δ変換やΔ-Y変換は三相交流で使われるΔ形回路とY形回路を相互に変換する変換である。
非対称なインピーダンスをもつ回路[編集]
本項では、非対称なインピーダンスをもつ回路を含む、一般のY-Δ変換・Δ-Y変換について説明する。
三相をとする。
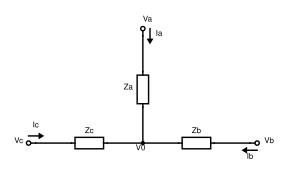 Y結線
Y結線
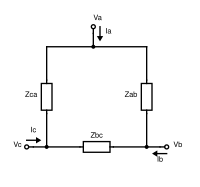 Δ結線
Δ結線
Y型回路の電圧を(は中性点の電圧),
Δ型回路のc→b→a方向の電圧を
キルヒホッフの電圧則より
Y型回路の中性点に流れ込む電流を,
Δ型回路のa→b→c方向の電流をとする。
キルヒホッフの電流則より
インピーダンス[編集]
Y型回路のインピーダンスを,
Δ型回路のインピーダンスをとする。
前述の電圧と電流およびオームの法則より
以下は詳しい導出である。
なので
である。これらは任意のについて成立するため、3式のの係数は一致するから
となる。整理して
よって
また、それぞれ
- とをに
- とをに
- とをに
代入して
よって
対称三相交流回路[編集]
三相交流では三つの電源(発電機のコイルと考えても、変圧器のコイルと考えてもよい)から3本の導線を使って負荷に電力を供給するものである。三相の接続は二つの方式がある。Yの形に接続したものをY接続または星形接続といい、Yの中心部である点Nを中性点という。この場合、それぞれ一つの電源が一つの負荷に電力を供給し、電流I1、I2、I3は3つの電源を出ていずれも中性点N同士を結ぶ導線を通って帰ると考える。
これに対して正三角形に接続したものをΔ接続または環状接続という。電力関係では、両方の接続方式ともよく用いられるが、、Y接続は主に送電線で用いられ、Δ接続は主に配電線で用いられる。
対称3相交流電圧のYーΔ変換[編集]
- Y接続の中性点からa相、b相、c相へ向かう電圧Va、Vb、Vcを相電圧または星形電圧という。
- Δ接続の正三角形の頂点a、b、cとの間の各相間(例えばa-b相間など)の電圧を線間電圧という。またY接続の各相間の電圧も線間電圧という。これをVab、Vbc、Vcaとする。
- 相電圧と線間電圧の関係は
とすると、三平方の定理より、
となる。つまり、相電圧√3VY=線間電圧VΔとなる。
また、対称3相交流電圧のフェーザ図からは、
=√3V∠30°=V1∠30°
=√3V∠-90°=V1∠-90°
=√3V∠150°=V1∠150°
対称3相交流電流のY-Δ変換[編集]
Δ接続の正三角形の頂点a、b、cから外部へ向かう電流
, ,
を線電流もしくは相電流という。また、Δ上を流れる電流
を環状電流という。
今、Iabを基準としてIab
=Ir∠0°とすると両者間の関係を示すフェーザ図を作成する。
中点Nから0°、-120°、120°からのベクトルを
とすると、キルヒホッフの第1則から、
となるので、次の式が得られる。
以上より次の関係が得られる。
線電流(相電流)I=環状電流Ir×√3
関連項目[編集]

