円 (数学)

円(えん)とは、ある中心点からの距離が等しいまま、曲線を集合した形。円周。平面上で一定の長さ(半径)にある点を限りなく細かくとった平面図形。正多角形の辺や角の数を無限大まで増やした図形ともいえる。

円周は、円の直径よりも長く、円周を直線にした場合、円周は直径より3.14倍長い。

円の起点は、円の上部の頂点、円の真上、円のスタート地点、円の始点であり、円周の角度で0°=360°の位置に当たる。比喩的に、円の頭、円の基本の位置に当たる。時計で表すと12時の位置である。

円の向きの進行方向には、右回りと左回りがある。右回りとは、円の上部の頂点（0°）から見て、右に向かって回る動きや、前進からの進行方向が右に向かって曲がることを意味する。左回りとは、円の上部の頂点（0°）から見て、左に向かって回る動きや、前進からの進行方向が左に向かって曲がることを意味する。

右回りへ進めば角度の数値は大きくなり、左回りへ進めば角度の数値は小さくなる。

車のハンドルを右回りにすると車が右に曲がり、車のハンドルを左回りにすると車が左に曲がる。左回り、右回りのメカニズムには、車の方向指示器も同様である。日本車は右ハンドルなので、車の方向指示器は、ハンドルの右に設置されており、方向指示器を上にすると左折、方向指示器を下にすると右折になる。理由は、円の進行方向・回転方向との役割があり、右から上に進むと左回り（左回転）、右から下に進むと右回り（右回転）と同じ役割を持つからである。右から上が左回りなのは、右から上に向かって円を描くような動きを指し、右から下が右回りなのは、右から下に向かって円を描くような動きを指すからである。

下から左は右回り、下から右は左回りになる。

右回り・左回りを、上下左右で表すと、右回りは、上から右、右から下、下から左、左から上。左回りは、上から左、左から下、下から右、右から上。

用語

• 直径 - 半径の2倍の長さ。円の中にとれる線分の中で最長。「外径」ともいう。
• 円周 - 円の周り。
• 弧 - 円周の一部。
• 弦 - 円周上にある二つの点を結んだ線分。

円周の長さ

半径 $r$ の円の円周は、

$2{\pi }r$ 

で求められる。 $\pi$ は円周率と呼ばれ、円周を直径で割った値がどんな円でも一定の値 3.14… となるため定数として扱われている。

円の面積

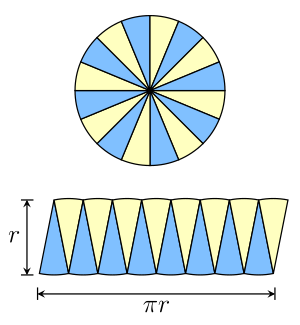
右の図のように、円板を扇形に刻んでそれらを互い違いに並べていく。扇形の分割数を限りなく増やすと底辺が $\pi r$、高さが $r$ の長方形（平行四辺形）とみなせるので、もとの円の面積が $S=\pi r^{2}$ で与えられることが分かる。

以下のように積分を使って導出することもできる。

半径 r の円は xy 平面上で $x^{2}+y^{2}=r^{2}$ の式で表される。これを y を x の式で表すと $y=\pm {\sqrt {r^{2}-x^{2}}}$ と変形できる。

ここで $y>0$ の領域だけ考えれば、この部分に含まれる面積はもとの円の 1/2 なので、円の面積 S は

${\frac {S}{2}}=\int _{-r}^{r}ydx$

のように表される。これを計算すると、

${\begin{aligned}S&=2\int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}dx\\&=\left[x{\sqrt {r^{2}-x^{2}}}+r^{2}\arcsin {\frac {x}{r}}\right]_{-r}^{r}\\&=r^{2}\arcsin 1-r^{2}\arcsin(-1)\\&=r^{2}\left({\frac {\pi }{2}}-{\frac {-\pi }{2}}\right)\\&=\pi r^{2}\end{aligned}}$

外部リンク

• [1]

関連項目

• 球 - ある円の中心を通りその円と同じ平面上に存在する直線周りに、その円を回転させた軌跡のような立体
• 円柱 - ある円の中心を通りその円と垂直な直線上の各点を中心とし、元の円と平行で、元の円と同じ半径の円を積み重ねたような立体
• 円錐 - ある円の中心を通りその円と垂直な直線上の各点を中心とし、元の円と平行で、半径を連続的に小さくしていった円を積み重ねたような立体
• 単位円 - 半径が単位長の円
• 右回転・左回転