二電力計法

二電力計法（にでんりょくけいほう）とは、三相3線式の平均電力を2個の電力計を用いて測定する方法。

概要

一般に$n$相$n$線式の電力は$(n-1)$個の単相電力計を用いて、それらの指示の代数和として求められる（ブロンデルの定理）。

測定原理

二電力計法の測定回路図

ベクトル図

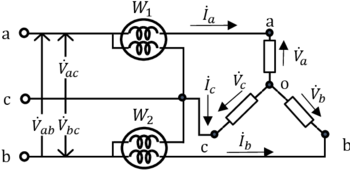
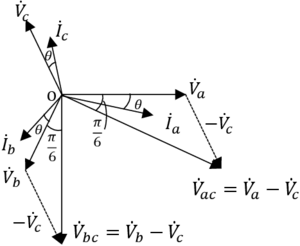
上図の平衡三相回路の三相電力を測定する二電力計法の測定回路において(対称三相Ｙ接続交流回路、平衝負荷なので負荷の各相インピーダンスがすべて等しい) 端子a, b, cのそれぞれの電位を$\dot{V_a},\dot{V_b},\dot{V_c}$ とし、線電流を$\dot{I_a},\dot{I_b},\dot{I_c}$とする。端子ab, bc, acの線間電圧をそれぞれ$\dot{V_{ab}},\dot{V_{bc}},\dot{V_{ac}}$とする。また、電力計を$W_1,W_2$とする。 $W_1$の電圧コイルに加わる電圧$\dot{V_{ac}}$は、 $\dot{V_a}-\dot{V_c}$であるから、下図のフェーザ図のようになり、 電流コイルに流れる電流$\dot{I_a}$との間には$\frac{\pi }{6}-\theta$ [rad]の位相差がある。また、電力計$W_2$の電圧コイルに加わる電圧$\dot{V_{bc}}$は$\dot{V_b}-\dot{V_c}$でベクトル図のようになり、 電流コイルに流れる電流$\dot{I_b}$との間には$\frac{\pi }{6}+\theta$ [rad]の位相差がある。したがって、$W_1$および$W_2$の指示をそれぞれ

$P_1$及び$P_2$とすれば

$P_1=V_{ac}{I}_a\cos (\frac{\pi }{6}-\theta )$

$P_2=V_{bc}{I}_b\cos (\frac{\pi }{6}+\theta )$

となる。対称三相交流であるから、

$V_{ab}=V_{bc}=V_{ca}=V$

$I_a=I_b=I_c=I$

の関係があるので

$P_1=VI\cos (\frac{\pi }{6}-\theta )$

$P_2=VI\cos (\frac{\pi }{6}+\theta )$

となる。したがって、三相電力Ｐは加法定理 (三角関数)より、

$P=P_1+P_2=VI\{\cos (\frac{\pi }{6}-\theta )+\cos (\frac{\pi }{6}+\theta )\}$

$=VI\{\cos \frac{\pi }{6}\cos \theta +\sin \frac{\pi }{6}\sin \theta +\cos \frac{\pi }{6}\cos \theta -\sin \frac{\pi }{6}\sin \theta \}$

$=2VI\cos \frac{\pi }{6}\cos \theta =2VI\cos \theta (\frac{\sqrt{3}}{2})$

$=\sqrt{3}VI\cos \theta$

となり、$W_1,W_2$の指示値の和が三相電力と等しくなる。

関連項目

• 交流
• 三相交流
• 交流回路

参考文献

• 酒井善雄『電気電子工学概論』丸善株式会社
• 矢野隆、大石隼人『発変電工学入門』森北出版株式会社2000年9月13日第1版第4刷発行
• 西巻正郎・森武昭・荒井俊彦『電気回路の基礎』森北出版株式会社1998年3月18日第1版第12刷発行